Getting Started

This guide covers the steps to get started with azcausal. We have split this introduction into several parts:

• Part I : The Panel

• Part II: The Treatment Effect

• Part III: Analysis & Visualization

Part I: Causal Panel

The very first step before doing any causal inference is get loading the data and tranforming them in the right format. Most estimators in this framework require the data to be in form of a Panel object.

Assuming we have the following data frame representing the CaliforniaProp99 information:

from azcausal.data import CaliforniaProp99

df = CaliforniaProp99().df()

df

	State	Year	PacksPerCapita	treated
0	Alabama	1970	89.800003	0
1	Arkansas	1970	100.300003	0
2	Colorado	1970	124.800003	0
3	Connecticut	1970	120.000000	0
4	Delaware	1970	155.000000	0
...	...	...	...	...
1204	Virginia	2000	96.699997	0
1205	West Virginia	2000	107.900002	0
1206	Wisconsin	2000	80.099998	0
1207	Wyoming	2000	90.500000	0
1208	California	2000	41.599998	1

1209 rows × 4 columns

In this example, the columns represent the following:

• The units: are given by each state (State)

• The time: is represented in years (Year)

• The outcome is the number of packs sold (PacksPerCapita)

• The intervention is indicated by the binary treatment column (treated)

We define a Panel as a data frame where the index represents time and each column a unit. We can extract the outcome from the data frame by:

from azcausal.util import to_panel

outcome = to_panel(df, "Year", "State", "PacksPerCapita")

outcome.head(3)

State	Alabama	Arkansas	California	Colorado	Connecticut	Delaware	Georgia	Idaho	Illinois	Indiana	...	South Carolina	South Dakota	Tennessee	Texas	Utah	Vermont	Virginia	West Virginia	Wisconsin	Wyoming
Year
1970	89.800003	100.300003	123.0	124.800003	120.000000	155.000000	109.900002	102.400002	124.800003	134.600006	...	103.599998	92.699997	99.800003	106.400002	65.500000	122.599998	124.300003	114.5	106.400002	132.199997
1971	95.400002	104.099998	121.0	125.500000	117.599998	161.100006	115.699997	108.500000	125.599998	139.300003	...	115.000000	96.699997	106.300003	108.900002	67.699997	124.400002	128.399994	111.5	105.400002	131.699997
1972	101.099998	103.900002	123.5	134.300003	110.800003	156.300003	117.000000	126.099998	126.599998	149.199997	...	118.699997	103.000000	111.500000	108.599998	71.300003	138.000000	137.000000	117.5	108.800003	140.000000

3 rows × 39 columns

To check whether the panel data are in fact balanced (we have an entry during each time step for each unit), we can check for NaN values in the data frame:

print("Is Balanced:", (~outcome.isna()).all(axis=None))

Is Balanced: True

Let us simulated some data would be missing

not_balanced = to_panel(df.head(80), "Year", "State", "PacksPerCapita")
print("Is Balanced:", (~not_balanced.isna()).all(axis=None))

not_balanced.head(3)

Is Balanced: False

State	Alabama	Arkansas	California	Colorado	Connecticut	Delaware	Georgia	Idaho	Illinois	Indiana	...	South Carolina	South Dakota	Tennessee	Texas	Utah	Vermont	Virginia	West Virginia	Wisconsin	Wyoming
Year
1970	89.800003	100.300003	123.0	124.800003	120.000000	155.000000	109.900002	102.400002	124.800003	134.600006	...	103.599998	92.699997	99.800003	106.400002	65.500000	122.599998	124.300003	114.5	106.400002	132.199997
1971	95.400002	104.099998	121.0	125.500000	117.599998	161.100006	115.699997	108.500000	125.599998	139.300003	...	115.000000	96.699997	106.300003	108.900002	67.699997	124.400002	128.399994	111.5	105.400002	131.699997
1972	101.099998	103.900002	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN

3 rows × 39 columns

Instead of extacting only one value at a time, we can also extract multiple directly by

from azcausal.util import to_panels

data = to_panels(df, "Year", "State", ["PacksPerCapita", "treated"])

data.keys()

dict_keys(['PacksPerCapita', 'treated'])

The reason why we have introduced an object called Panel is to combine multiple data frames into one and to have convinient access to information about the time pre and post experiment, as well as control and treatment units. A Panel can be created by passing the outcome and intervention directly as pd.DataFrame:

from azcausal.core.panel import CausalPanel

panel = CausalPanel(data=data).setup(outcome='PacksPerCapita', intervention='treated')

print(panel.summary())

╭──────────────────────────────────────────────────────────────────────────────╮
|                                    Panel                                     |
|  Time Periods: 31 (19/12)                                  total (pre/post)  |
|  Units: 39 (38/1)                                       total (contr/treat)  |
╰──────────────────────────────────────────────────────────────────────────────╯

The panel allows accessing outcome and intervention directly trough properties:

panel.outcome.head(3)

State	Alabama	Arkansas	California	Colorado	Connecticut	Delaware	Georgia	Idaho	Illinois	Indiana	...	South Carolina	South Dakota	Tennessee	Texas	Utah	Vermont	Virginia	West Virginia	Wisconsin	Wyoming
Year
1970	89.800003	100.300003	123.0	124.800003	120.000000	155.000000	109.900002	102.400002	124.800003	134.600006	...	103.599998	92.699997	99.800003	106.400002	65.500000	122.599998	124.300003	114.5	106.400002	132.199997
1971	95.400002	104.099998	121.0	125.500000	117.599998	161.100006	115.699997	108.500000	125.599998	139.300003	...	115.000000	96.699997	106.300003	108.900002	67.699997	124.400002	128.399994	111.5	105.400002	131.699997
1972	101.099998	103.900002	123.5	134.300003	110.800003	156.300003	117.000000	126.099998	126.599998	149.199997	...	118.699997	103.000000	111.500000	108.599998	71.300003	138.000000	137.000000	117.5	108.800003	140.000000

3 rows × 39 columns

or using the index function by

panel['outcome'].head(3)

State	Alabama	Arkansas	California	Colorado	Connecticut	Delaware	Georgia	Idaho	Illinois	Indiana	...	South Carolina	South Dakota	Tennessee	Texas	Utah	Vermont	Virginia	West Virginia	Wisconsin	Wyoming
Year
1970	89.800003	100.300003	123.0	124.800003	120.000000	155.000000	109.900002	102.400002	124.800003	134.600006	...	103.599998	92.699997	99.800003	106.400002	65.500000	122.599998	124.300003	114.5	106.400002	132.199997
1971	95.400002	104.099998	121.0	125.500000	117.599998	161.100006	115.699997	108.500000	125.599998	139.300003	...	115.000000	96.699997	106.300003	108.900002	67.699997	124.400002	128.399994	111.5	105.400002	131.699997
1972	101.099998	103.900002	123.5	134.300003	110.800003	156.300003	117.000000	126.099998	126.599998	149.199997	...	118.699997	103.000000	111.500000	108.599998	71.300003	138.000000	137.000000	117.5	108.800003	140.000000

3 rows × 39 columns

panel.intervention.tail(3)

State	Alabama	Arkansas	California	Colorado	Connecticut	Delaware	Georgia	Idaho	Illinois	Indiana	...	South Carolina	South Dakota	Tennessee	Texas	Utah	Vermont	Virginia	West Virginia	Wisconsin	Wyoming
Year
1998	0	0	1	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
1999	0	0	1	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
2000	0	0	1	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0

3 rows × 39 columns

Moreover, the method also allows to use the most common pandas functions on ALL DATA at once:

new_panel = panel.iloc[:, :3]

new_panel.outcome.head(3)

State	Alabama	Arkansas	California
Year
1970	89.800003	100.300003	123.0
1971	95.400002	104.099998	121.0
1972	101.099998	103.900002	123.5

Also, we can use the get method with key word arguments.

• if contr == True then only control units are returned.

• if treat == True then units which have been treated at least once are returned.

• if pre == True then time steps where no unit is treated is returned.

• if post == True then the time steps where at least one unit is treated.

, for example:

panel.filter(target='outcome', post=True, treat=True).head(3)

State	California
Year
1989	82.400002
1990	77.800003
1991	68.699997

For more methods please check the Panel immplementation directly.

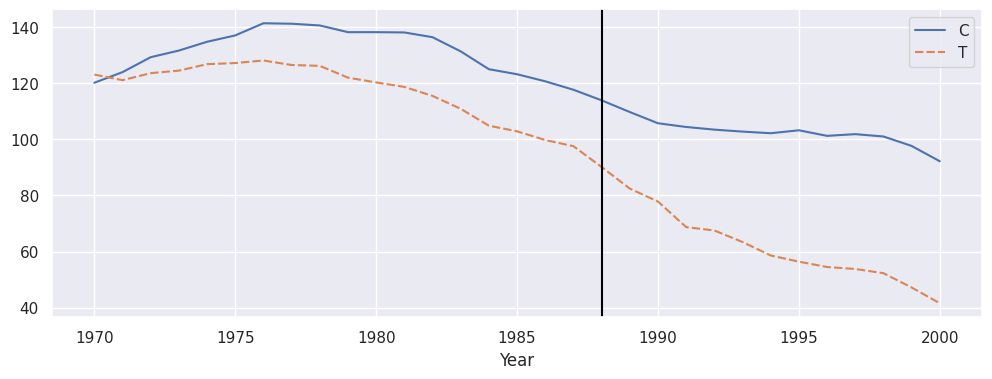
Using the CausalPanel it is also relatively easy to plot the average control versus treatment by:

import seaborn as sns
sns.set(rc={'figure.figsize':(12,4)})

import matplotlib.pyplot as plt

avg_control = panel.filter(target='outcome', contr=True).mean(axis=1).to_frame('C')
avg_treat = panel.filter(target='outcome', treat=True).mean(axis=1).to_frame('T')

plt.subplots(1, 1, figsize=(12, 4))
sns.lineplot(avg_control.join(avg_treat))
plt.axvline(panel.filter(target="intervention", pre=True).index.max(), color='black', label='intervention')

<matplotlib.lines.Line2D at 0x7fd4bda4c4c0>

Part II: The Treatment Effect

After bringing the data into the right format, we can use an Estimator to make predictions of the treatment effect.

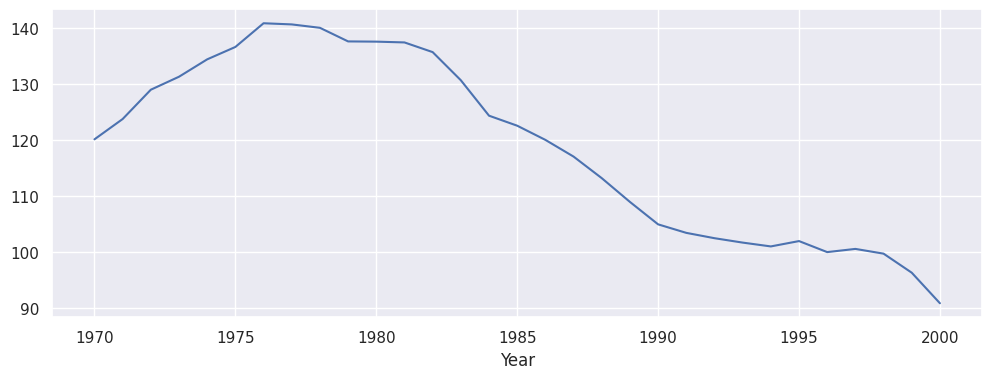
Like commonly done for time series it is always a good idea to quickly spot check the time series:

print(panel.summary())

panel.outcome.mean(axis=1).plot(figsize=(12, 4))

╭──────────────────────────────────────────────────────────────────────────────╮
|                                    Panel                                     |
|  Time Periods: 31 (19/12)                                  total (pre/post)  |
|  Units: 39 (38/1)                                       total (contr/treat)  |
╰──────────────────────────────────────────────────────────────────────────────╯

<Axes: xlabel='Year'>

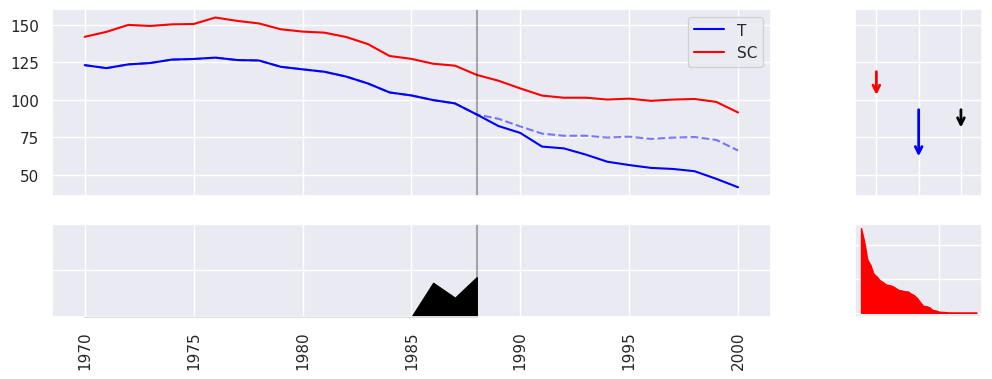
For example, let us use the popular DID estimator to estimate the Average Treatment Effect on the Treated (ATT) for the panel data.

from azcausal.estimators.panel.did import DID

# initialize an estimator object
estimator = DID()

# estimate the treatment effect
result = estimator.fit(panel)

# print the treatment effect summary
print(result.summary(percentage=True, cumulative=True))

╭──────────────────────────────────────────────────────────────────────────────╮
|                                    Panel                                     |
|  Time Periods: 31 (19/12)                                  total (pre/post)  |
|  Units: 39 (38/1)                                       total (contr/treat)  |
├──────────────────────────────────────────────────────────────────────────────┤
|                                     ATT                                      |
|  Effect: -27.35                                                              |
|  Observed: 60.35                                                             |
|  Counter Factual: 87.70                                                      |
├──────────────────────────────────────────────────────────────────────────────┤
|                                  Percentage                                  |
|  Effect: -31.19                                                              |
|  Observed: 68.81                                                             |
|  Counter Factual: 100.00                                                     |
├──────────────────────────────────────────────────────────────────────────────┤
|                                  Cumulative                                  |
|  Effect: -328.19                                                             |
|  Observed: 724.20                                                            |
|  Counter Factual: 1,052.39                                                   |
╰──────────────────────────────────────────────────────────────────────────────╯

Now, the treatment effect without any confidence intervals is often not that helpful. Some estimators come with error estimates out of the box and will directly provide them (e.g. DIDRegression). For others, we can use an Error estimator to attach an error and calculate confidence intervals along with it.

The following error estimators are available:

• Bootstrap: Randomly sample units (with replacement) from the panel data and estimate the effect.

• Placebo: Only sample from control units as use them as placebo.

• JackKnife: Leave one out crossvalidation but removing one unit at a time.

Each error estimate requires a treatment estimated on a new panel derived from the original data set by the corresponding method.

Each estimator has a method called estimator.error(result, method) which takes the original Result object returned before and the Error estimation method that should be used.

from azcausal.core.error import Bootstrap

se, runs = estimator.error(result, Bootstrap(n_samples=500))

print(result.summary(conf=90))

╭──────────────────────────────────────────────────────────────────────────────╮
|                                    Panel                                     |
|  Time Periods: 31 (19/12)                                  total (pre/post)  |
|  Units: 39 (38/1)                                       total (contr/treat)  |
├──────────────────────────────────────────────────────────────────────────────┤
|                                     ATT                                      |
|  Effect (±SE): -27.35 (±2.7923)                                              |
|  Confidence Interval (90%): [-31.94 , -22.76]                           (-)  |
|  Observed: 60.35                                                             |
|  Counter Factual: 87.70                                                      |
├──────────────────────────────────────────────────────────────────────────────┤
|                                  Percentage                                  |
|  Effect (±SE): -31.19 (±3.1839)                                              |
|  Confidence Interval (90%): [-36.42 , -25.95]                           (-)  |
|  Observed: 68.81                                                             |
|  Counter Factual: 100.00                                                     |
├──────────────────────────────────────────────────────────────────────────────┤
|                                  Cumulative                                  |
|  Effect (±SE): -328.19 (±33.51)                                              |
|  Confidence Interval (90%): [-383.30 , -273.07]                         (-)  |
|  Observed: 724.20                                                            |
|  Counter Factual: 1,052.39                                                   |
╰──────────────────────────────────────────────────────────────────────────────╯

Similarly, we can use SDID as an estimator

from azcausal.estimators.panel.sdid import SDID
from azcausal.core.error import JackKnife

# initialize an estimator object
estimator = SDID()

# estimate the treatment effect
result = estimator.fit(panel)

# here we use JackKnife which is optmized to be run with SDID
estimator.error(result, JackKnife())

# print the treatment effect summary
print(result.summary(percentage=True, cumulative=True))

╭──────────────────────────────────────────────────────────────────────────────╮
|                                    Panel                                     |
|  Time Periods: 31 (19/12)                                  total (pre/post)  |
|  Units: 39 (38/1)                                       total (contr/treat)  |
├──────────────────────────────────────────────────────────────────────────────┤
|                                     ATT                                      |
|  Effect (±SE): -15.60 (±2.9161)                                              |
|  Confidence Interval (95%): [-21.32 , -9.8884]                          (-)  |
|  Observed: 60.35                                                             |
|  Counter Factual: 75.95                                                      |
├──────────────────────────────────────────────────────────────────────────────┤
|                                  Percentage                                  |
|  Effect (±SE): -20.54 (±3.8393)                                              |
|  Confidence Interval (95%): [-28.07 , -13.02]                           (-)  |
|  Observed: 79.46                                                             |
|  Counter Factual: 100.00                                                     |
├──────────────────────────────────────────────────────────────────────────────┤
|                                  Cumulative                                  |
|  Effect (±SE): -187.25 (±34.99)                                              |
|  Confidence Interval (95%): [-255.83 , -118.66]                         (-)  |
|  Observed: 724.20                                                            |
|  Counter Factual: 911.45                                                     |
╰──────────────────────────────────────────────────────────────────────────────╯

Part III: Analysis & Visualization

Lastly, we want to give some idea on how to visualize results.

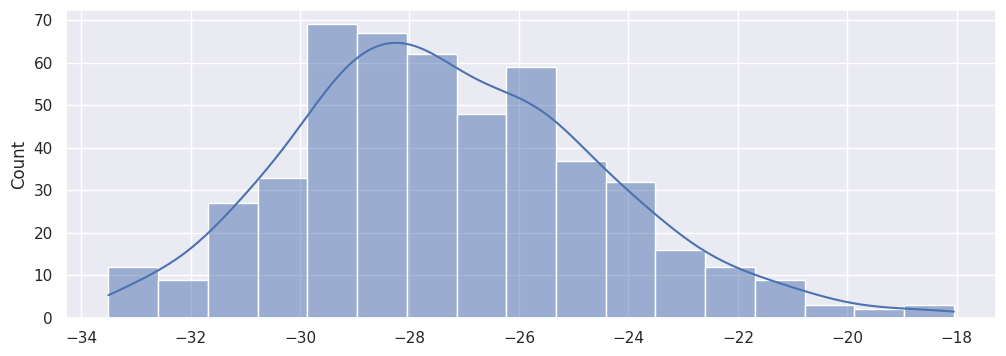
To learn more about how the error estimation was originally derived, we can check the corresponding distribution by plotting the estimates of each of the runs:

vv = [run.effect.value for run in runs]
sns.histplot(vv, kde=True)

<Axes: ylabel='Count'>

Each post-analysis will be different depending on the estimator. We would like a give an example of SDID here. The available additional information stored by the estimator are:

effect = result.effect

effect.data.keys()

dict_keys(['did', 'lambd', 'omega', 'solvers', 'error'])

The DID results give us additional information about how the ATT is actually calculated:

effect['did']

{'att': -15.603827872733866,
 'delta_contr': -19.192040932672626,
 'delta_treat': -34.79586880540649,
 'pre_contr': 120.49828909527162,
 'post_contr': 101.30624816259899,
 'pre_treat': 95.14586886957316,
 'post_treat': 60.35000006416667}

The unit weights (omega) with at least 1% contribution

effect['omega'].sort_values(ascending=False).loc[lambda x: x >= 0.01]

Nevada            0.124489
New Hampshire     0.105048
Connecticut       0.078287
Delaware          0.070368
Colorado          0.057513
Illinois          0.053388
Nebraska          0.047853
Montana           0.045135
Utah              0.041518
New Mexico        0.040568
Minnesota         0.039495
Wisconsin         0.036667
West Virginia     0.033569
North Carolina    0.032805
Idaho             0.031468
Ohio              0.031461
Maine             0.028211
Iowa              0.025939
Kansas            0.021605
Pennsylvania      0.015352
Indiana           0.010135
Name: omega, dtype: float64

Similarly, the time weights

effect['lambd'].sort_values(ascending=False).loc[lambda x: x >= 0.01]

1988    0.427076
1986    0.366471
1987    0.206453
Name: lambd, dtype: float64

Or in general the treatment effect over time:

# Control (C), Treatment (T), Time Weights (lambd), Intervention (W), Average Treatment Effect on the Treated (att), Counter Factual (CF)
effect.by_time.tail(5)

	C	T	post	att	CF
Year
1996	99.202557	54.500000	True	-19.350137	73.850137
1997	100.035935	53.799999	True	-20.883516	74.683515
1998	100.433993	52.299999	True	-22.781573	75.081573
1999	98.497346	47.200001	True	-25.944925	73.144926
2000	91.437300	41.599998	True	-24.484882	66.084880

effect.by_time[['C', 'CF', 'T']].head(3)

	C	CF	T
Year
1970	141.885954	123.0	123.0
1971	145.202800	121.0	121.0
1972	149.827472	123.5	123.5

Some estimators will have directly a plotting method for the result:

estimator.plot(result, show=False, CF=True)
None